Atualmente, conexionismo significa redes neurais, sendo neural uma referência aos neurônios biológicos. Apesar do nome, a relação entre ambos é pouco significativa.
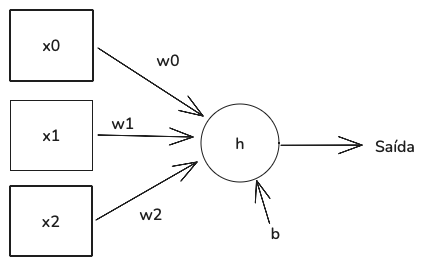
A figura acima representa um neurônio artificial. As entradas estão à esquerda, e o fluxo de dados à direita.
- Entradas: os três quadrados (xo, x1 e x2). Representam as três features de um vetor.
- Função de ativação: o círculo rotulado como h. Sua tarefa é aceitar a entrada para o neurônio e gerar um valor de saída (seta indo para a direita).
- Conexões entre as entradas e a função de ativação: os quadrados são ligados ao círculo por setas (wo, w1 e w2). Elas são os pesos. Cada entrada do neurônio possui um peso associado.
- Viés: o “b” conectado ao círculo. É um número, assim como os pesos, os Xs de entrada e de saída.
Este é o funcionamento do neurônio:
- Multiplica-se cada valor de entrada (xo, x1, x2) pelo seu peso associado (w0, w1, w2).
- Soma-se todos os produtos da etapa acima ao valor do viés “b”, gerando um único número.
- Fornece-se um número para a função de ativação “h”, a fim de gerar o número de saída.
É isso que o neurônio faz: multiplica suas entradas pelos pesos, soma os produtos, soma o valor de viés e passa esse valor para a função de ativação, visando gerar a saída.
É normal que as redes neurais utilizem a unidade linear retificadora (ReLU) como função de ativação. Ela é uma pergunta: a entrada é menor que zero? Se for, a saída é zero; caso contrário, é qualquer que seja a entrada.
Os neurônios são organizados em camadas: as saídas das camadas anteriores são as entradas da camada seguinte. Esta organização simplifica a implementação em código e facilita o procedimento padrão de treinamento.
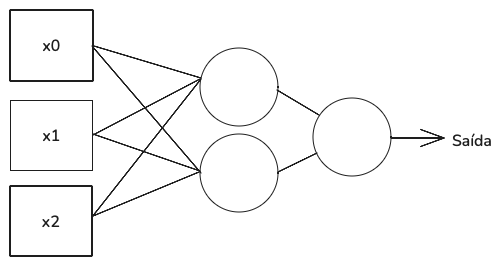
A imagem acima apresenta uma rede com dois nós. Temos três entradas (quadrados), dois círculos na camada intermediária e um círculo à direita. As entradas conectam-se aos dois nós da camada intermediária. As saídas da camada intermediária são conectadas a um único nó no canto direito, de onde se origina a saída da rede. Estas camadas intermediárias são conhecidas como camadas ocultas.
Uma rede como esta é adequada para tarefas de classificação binária, classe 0 ou 1, em que a saída é um único número representando a confiança do modelo de que a enteada é um membro de classe 1. O nó mais à direita usa uma função de ativação diferente, conhecida como sigmoide. Ela gera uma saída entre 0 e 1. Todos os nós da camada oculta permanecem usando função ReLU.
Quantos pesos e vieses deve-se aprender para implementar a rede acima? Necessita-se de um peso para cada linha (exceto a seta de saída) e um valor de viés para cada nó. Então, precisa-se de oito pesos e três valores de viés. À medida que o número de nós em uma camada aumenta, o número de pesos aumenta com mais rapidez.
Vamos simular o funcionamento desta rede tentando diferenciar duas variedades de uvas. Consideramos três features (xo, x1 e x2), sendo: graduação alcoólica (em %), ácido málico e fenóis totais. O modelo é treinado com 104 amostras e testado com 26 amostras. O conjunto de treinamento preparou o modelo de dois neurônios para fornecer valores a todos os 8 pesos e 3 vieses. Após treinado, o modelo alcançou precisão de 81%. A figura abaixo apresenta o modelo treinado, com os valores de pesos e vieses.
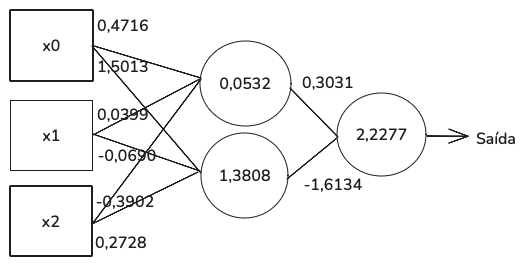
Vamos submeter o modelo a duas amostras de teste para entender o processo (x0, x1 e x2).
- Amostra 1 (-0,7359, 0,9795, -0,1333)
- Amostra 2 (0,0967, –1,2138, –1,0500)
A primeira feature é o percentual de graduação alcoólica. Na amostra 1, este número é negativo. Como isso é possível? Esperava-se um valor percentual. Isso se deve ao pré-processamento. Dados brutos, como a porcentagem de graduação alcoólica, geralmente não são utilizados em modelos de machine learning em seu formato original. Cada feature é ajustada, subtraindo o valor médio da feature no conjunto de treinamento e dividindo o resultado pela medida de dispersão dos dados em torno do valor médio (desvio-padrão). O valor original de 12,29% de graduação alcoólica tornou-se -0,7359.
Cada feature (entrada do neurônio) é multiplicada pelo peso na linha que a conecta ao neurônio e, em seguida, somada ao valor de viés. Então temos:
(0,4716 * -0,7359) – primeira feature
+ (0,0399 * 0,9795) – segunda feature
+ (-0,3902 x -0,1333) – terceira feature
+ 0,0532 – viés
Obtemos o resultado de -0,2028. É o número passado para a função de ativação, uma ReLU. Sendo negativo, a ReLU retorna 0, o que significa que a saída do nó superior é 0. Para o nó inferior, temos o resultado de 0,1720. Sendo um número positivo, a ReLU retorna 0,1720 como saída. Na camada intermediária, as saídas dos dois nós são usadas como entradas para o nó final à direita. Agora a função de ativação é uma sigmoide.
A saída do nó superior é 0 e a saída do nó inferior é 0,1720. Quando os multiplicamos por seus respectivos pesos, somados ao valor de viés de 2,2277, obtemos 1,9502 como argumento para a função de ativação sigmoide, gerando 0,8755 como saída da rede para a primeira amostra de entrada.
Este resultado é um valor percentual, indicando 87% de confiança de que essa entrada representa uma instância da classe 1. Geralmente adotamos o limiar de 50%. Se a saída for maior que 50%, atribuímos a entrada à classe 1.
Repetindo o exercício para a classe 2, temos o resultado de 0,4883. Com um limiar de 50%, rejeitamos o rótulo da classe 1 e atribuímos a amostra 2 à classe 0. Mas a classe real é 1, então a rede está errada!
Poderíamos adotar como limiar o valor de 40%, não 50%. Então, capturaríamos mais entradas da classe 1, mesmo identificando erroneamente mais amostras reais de classe 0 como classe 1. Trocaríamos um tipo de erro por outro.
Em nossos experimentos, quais seriam os resultados com redes de mais nós? Foram testadas outras redes, em um processo com 240 execuções, gerando as seguintes médias de acurácia:
- 2 nós: 81,5%
- 3 nós: 83,6%
- 8 nós: 86,2%
As redes neurais são aleatoriamente inicializadas, então o treinamento repetido leva a modelos com desempenho diferente, mesmo utilizando o mesmo conjunto de dados de treinamento. “Aleatoriamente inicializadas” quer dizer que os números dos pesos e vieses são originados de um processo iterativo: o conjunto inicial dos números de pesos e vieses é atualizado repetidamente. A cada atualização, a rede se aproxima mais de qualquer função que conecta os vetores de feature de entrada e os rótulos de saída.
Escolhendo um conjunto aleatório diferente de pesos e viés inicial fará com que a rede convirja para um conjunto diferente de valores finais. A rede de 2 nós alcançou acurácia de 81%, mas considerando sessões de treinamento com diferentes pesos e vieses iniciais, a acurácia variou entre 73% e 89%.
Na parte 2 do documento sobre redes neurais, explicaremos de onde se originam os valores dos pesos e vieses.
Referências
Kneusel, Ronald T.. Como a Inteligência Artificial Funciona: Da Magia à Ciência
Comments (0)