Chegamos ao terceiro e último artigo sobre os modelos clássicos de machine learning tradicional. Já conhecemos os modelos de vizinhos mais próximos e as árvores de decisão. Hoje, abordaremos as máquinas de vetores de suporte.
Máquinas de vetores de suporte (SVM)
Para entender as máquinas de vetores de suporte é necessário compreender quatro conceitos: margens, vetores de suporte, otimização e kernels. Retomaremos o conjunto de dados da flor de íris. Novamente, consideraremos setosa (círculo) e versicolor (quadrado), com vetores bidimensionais de features (comprimento da pétala e largura da pétala).
Seria simples criar um classificador para esse conjunto de dados, visto que uma linha separaria facilmente o conjunto de dados por classe. Mas qual seria o local adequado para essa linha? Podemos usar um número infinito de linhas. Devemos posicionar a linha de separação o mais longe possível de cada grupo. E aqui entra a máquina de vetores de suporte – SVM. As SVMs tentam maximizar a margem entre os dois grupos, encontrando o local com a maior separação entre as classes. Quando identificam a margem máxima, elas inserem a fronteira – nesse exemplo, uma linha – no meio da margem, porque é o mais sensato a fazer com base nas informações contidas nos dados de treinamento.
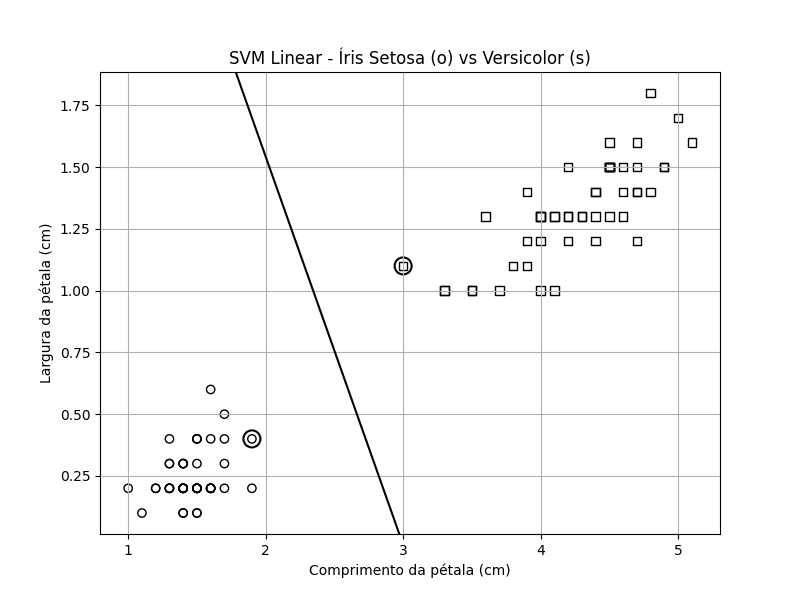
A figura abaixo apresenta os dados de treinamento com a linha adicional, que sinaliza a fronteira inserida pela SVM para maximizar a distância entre as classes. É a melhor posição para a linha minimizar erros de rotulagem entre as duas classes. Em resumo, isso é tudo que uma SVM faz.
As outras três partes de uma SVM — vetores de suporte, otimização e kernels — são usadas para encontrar as margens e a linha de separação. Observe que alguns dos pontos de dados estão destacados. Esses pontos são os vetores de suporte que o algoritmo encontra para definir a margem e a partir daí a linha de separação. De onde vêm esses vetores de suporte? Os vetores de suporte são membros do conjunto de treinamento encontrados por meio de um algoritmo de otimização. A otimização busca o melhor de algo, de acordo com critérios definidos. O algoritmo de otimização usado por uma SVM localiza os vetores de suporte que definem a margem máxima e, em última análise, a linha de separação.
Para replicar a figura acima, o seguinte código Python pode ser utilizado:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
# Carregar o dataset da íris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Selecionar apenas as classes Setosa (0) e Versicolor (1)
mask = y < 2
X = X[mask]
y = y[mask]
# Usar comprimento e largura da pétala (índices 2 e 3)
X = X[:, 2:4]
# Criar e treinar o modelo SVM linear
clf = SVC(kernel='linear')
clf.fit(X, y)
# Obter coeficientes da reta de separação
w = clf.coef_[0]
b = clf.intercept_[0]
# Função para plotar linha de separação
def plot_decision_boundary(X, y, clf):
plt.figure(figsize=(8, 6))
# Plotar Setosa (círculo sem preenchimento)
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1],
marker='o', facecolors='none', edgecolors='k', label='Setosa')
# Plotar Versicolor (quadrado sem preenchimento)
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1],
marker='s', facecolors='none', edgecolors='k', label='Versicolor')
# Linha de decisão
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1])
yy = -(w[0] * xx + b) / w[1]
# Margens (1 distância do hiperplano)
margin = 1 / np.linalg.norm(w)
yy_down = yy - np.sqrt(1 + (w[0]/w[1])**2) * margin
yy_up = yy + np.sqrt(1 + (w[0]/w[1])**2) * margin
# Plotar linhas
plt.plot(xx, yy, 'k-', label="Linha de separação")
# Vetores de suporte (círculos grandes, sem preenchimento)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=150, facecolors='none', edgecolors='k', linewidths=1.5,
label='Vetores de suporte')
plt.xlabel("Comprimento da pétala (cm)")
plt.ylabel("Largura da pétala (cm)")
plt.title("SVM Linear - Íris Setosa (o) vs Versicolor (s)")
plt.grid(True)
plt.xlim(xlim)
plt.ylim(ylim)
plt.savefig('svm0.png', transparent=True)
plt.show()
# Chamar função de plotagem
plot_decision_boundary(X, y, clf)Os kernels matemáticos estabelecem relacionamentos entre duas entidades. Nosso exemplo utiliza um kernel linear. Usa os vetores de feature de dados de treinamento como eles são. O kernel transforma os vetores de feature em uma representação diferente, base fundamental para o que as redes neurais convolucionais fazem.
Os profissionais de machine learning clássico se empenharam consideravelmente a fim de tentar minimizar o número de features necessárias para um modelo, reduzindo-as ao conjunto mínimo necessário para que o modelo distinguisse as classes. Essa abordagem passou a ser chamada de seleção de features ou de redução de dimensionalidade. Da mesma forma, sobretudo com as SVMs, os kernels foram usados a fim de mapear determinados vetores de feature para uma nova representação, facilitando a separação de classes. Na prática, treinar uma máquina de vetores de suporte significa localizar bons valores para os parâmetros relacionados ao kernel usado.
As SVMs são classificadores binários: elas distinguem duas classes. Mas, e se precisarmos distinguir mais de duas classes?
Temos duas opções de generalizar SVMs para problemas multiclasse.
One-versus-Rest (OvR)
Imagine que temos dez classes no conjunto de dados. A primeira abordagem de generalização treina 10 SVMs, a primeira tenta separar a classe 0 das outras nove classes. A segunda abordagem também tenta separar a classe 1 das nove classes restantes, e assim por diante, fornecendo-nos uma coleção de modelos, cada um tentando separar uma classe de todas as outras. Para classificar uma amostra desconhecida, fornecemos a amostra a cada SVM e retornamos o rótulo da classe do modelo que gerou o maior valor da função de decisão – a métrica que a SVM usa para decidir sua confiança em sua saída. Essa estratégia é conhecida como one-versus-rest (OvR) ou one-versus-all. Com ela, podemos treinar SVMs e classes.
Vantagens
- Mais simples: só precisa treinar N classificadores (onde N é o número de classes).
- Mais rápido no treinamento, se N for pequeno.
Desvantagens
- Pode ter desequilíbrio de dados (ex: 1 classe contra muitas).
- Pode ser menos preciso em cenários complexos.
Exemplo
- SVM1: Gato vs (Cachorro + Coelho)
- SVM2: Cachorro vs (Gato + Coelho)
- SVM3: Coelho vs (Gato + Cachorro)
One-versus-One (OvO)
A outra estratégia se chama one-versus-one, que treina uma SVM separada para cada par possível de classes. A amostra desconhecida é fornecida a cada modelo e o rótulo de classe que aparece com mais frequência é atribuído a ela.
Vantagens
- Os classificadores são mais focados, pois lidam só com dois tipos de dados.
- Costuma ter melhor performance em alguns cenários.
Desvantagens
- Precisa treinar N(N – 1)/2 classificadores – cresce rápido com o número de classes.
- Mais complexo e pode ser mais demorado.
Exemplo
- SVM1: Gato vs Cachorro
- SVM2: Gato vs Coelho
- SVM3: Cachorro vs Coelho
Referências
Kneusel, Ronald T.. Como a Inteligência Artificial Funciona: Da Magia à Ciência
Comments (0)