Esta é a segunda parte de nosso texto sobre visão geral da IA. Na primeira parte, fomos apresentados aos primeiros conceitos de IA. Aprendemos a importância de vetores e matrizes para machine learning. E, a partir do exemplo da Flor de Íris, entendemos que algumas classificações são simples, como a distinção entre I. setosa e I. versicolor. Mas outras são mais difíceis, como a distinção entre I. versicolor e I. virginica. Vamos em frente …
Quando o conjunto de exemplos não possui todas as entradas possíveis no mundo real
Passemos a um novo experimento. Um popular conjunto de dados usado por todos os pesquisadores de IA tem dezenas de milhares de pequenas imagens com algarismos escritos à mão, de 0 a 9. Chama-se MNIST (Modified NIST). Na figura abaixo, podemos ver algumas típicas amostras de algarismos do MNIST. Os vetores de feature de entrada são imagens de algarismos convertidas em vetores; a primeira linha de pixels é seguida pela segunda linha, depois pela terceira e assim por diante. As imagens dos algarismos têm 28×28 pixels, gerando um vetor de feature com 784 números – estamos instruindo à rede neural que aprenda coisas em um espaço de 784 dimensões.

Por Suvanjanprasai – Obra do próprio, CC BY-SA 4.0, Hiperligação
Nosso objetivo é criar uma rede neural que aprenda a identificar os algarismos 0, 1, 3 e 9. Utilizando Python e o subconjunto MNIST da biblioteca Sklearn, treinaremos a rede com aproximadamente 144 amostras para cada algarismo. E a testaremos com aproximadamente 36 amostras para cada algarismo (20% do total de amostras).
Utilizamos uma tabela bidimensional – matriz de confusão – para avaliar o modelo. A matriz de confusão resultante é demonstrada abaixo.
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
import matplotlib.pyplot as plt
import numpy as np
# Carregar o conjunto de dígitos MNIST reduzido (8x8) do sklearn
digits = load_digits()
# Filtrar apenas os dígitos 0, 1, 3 e 9
selected_classes = [0, 1, 3, 9]
mask = np.isin(digits.target, selected_classes)
X = digits.data[mask]
y = digits.target[mask]
# Dividir em conjunto de treino e teste
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42, stratify=y
)
# Treinar classificador (árvore de decisão como exemplo)
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)
# Fazer predições
y_pred = clf.predict(X_test)
# Calcular matriz de confusão
cm = confusion_matrix(y_test, y_pred, labels=selected_classes)
# Exibir a matriz
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=selected_classes)
disp.plot(cmap='Grays')
plt.title("Matriz de Confusão - Algarismos 0, 1, 3 e 9")
plt.savefig('matriz_confusao_mnist1.png', transparent=True)
plt.show()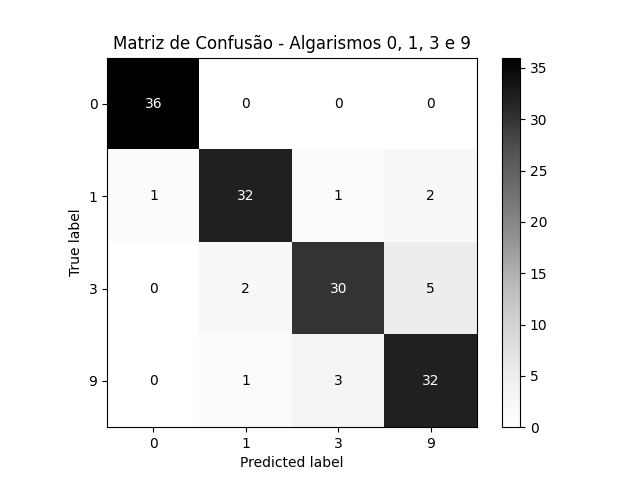
As linhas da matriz representam os rótulos verdadeiros [True label – ground truth] para as amostras fornecidas ao modelo. As colunas são as respostas do modelo. Os valores da tabela são contagens, o número de vezes que cada combinação possível de classe de entrada e rótulo atribuído ao modelo aconteceu. A primeira linha representa os zeros no conjunto de teste. Dessas 36 entradas de teste, o modelo retornou um rótulo adequado para todas elas. Quando zero foi a entrada, a saída do modelo acertou 100%.
Após treinar o classificador, vamos apresentar imagens (36 amostras) de algarismos 4 e 7, para os quais ele não foi treinado. O que ele poderia fazer com essas entradas?
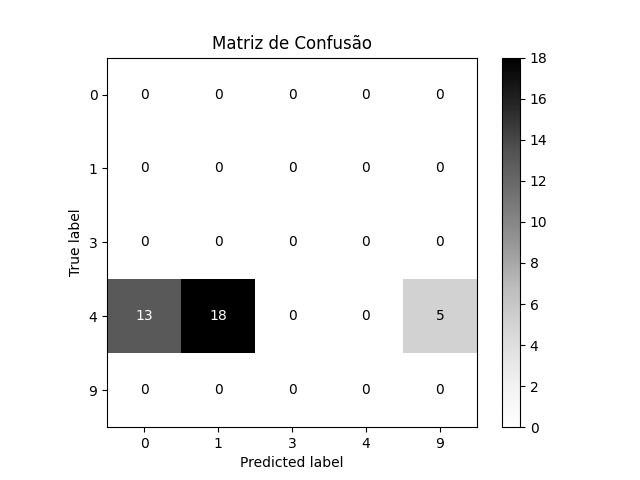
O modelo aplicou o rótulo 0 para 13 amostras de algarismo 4, o rótulo 1 para 18 amostras e o rótulo 9 para 5 amostras. Para o número 7, a distribuição é apresentada na tabela a seguir.
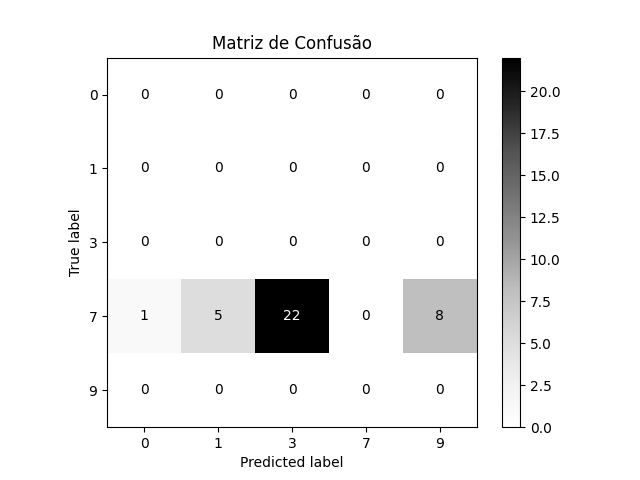
Como nunca foi ensinado a reconhecer os números 4 e 7, o modelo optou por aquilo que considerou a segunda melhor opção.
Interpolação e extrapolação
Também é importante falarmos sobre interpolação e extrapolação. A interpolação se aproxima do intervalo de dados conhecidos e a extrapolação vai além dos dados conhecidos. Interpolar é como “preencher o meio”, prever entre os dados. Extrapolar é como “esticar a linha para fora”, prever além dos dados, fora do intervalo conhecido.
Vamos tomar como exemplo a população mundial de 1950 a 2020. Ajustaremos uma linha a estes dados; trata-se de uma forma de ajuste de curva. A figura abaixo apresenta uma linha (linha tracejada) que acompanha o crescimento populacional mundial (População (bilhões)), representado por círculos. Como a linha passa por ou bem perto de quase todos os sinais, o ajuste é razoável. Tendo a linha, podemos usar a inclinação (coeficiente angular) e o intercepto (ponto em que a linha cruza o eixo y) para estimar a população de qualquer ano. A estimativa para os anos 1950 a 1970 é uma interpolação, pois usamos dados desse intervalo de anos para criar a linha. Se estimamos populações anteriores ou posteriores a esse período, estamos extrapolando.
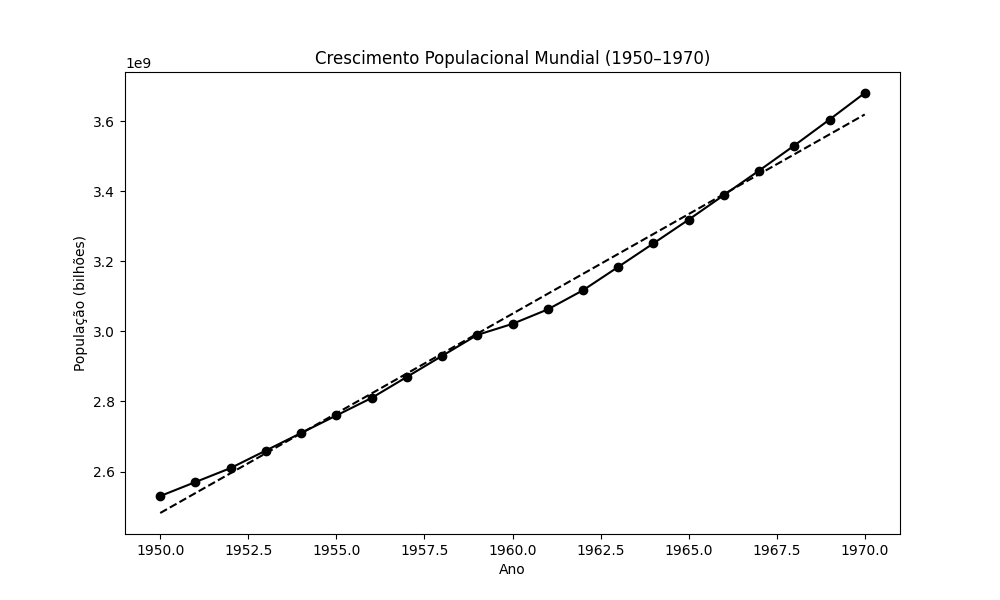
Vamos extrapolar para datas fora do intervalo de ajuste, conforme demonstrado na figura a seguir. A diferença entre os valores populacionais extrapolados (linha tracejada) e a população efetiva (linha com círculos) aumenta a cada ano. O modelo não funcionou bem.
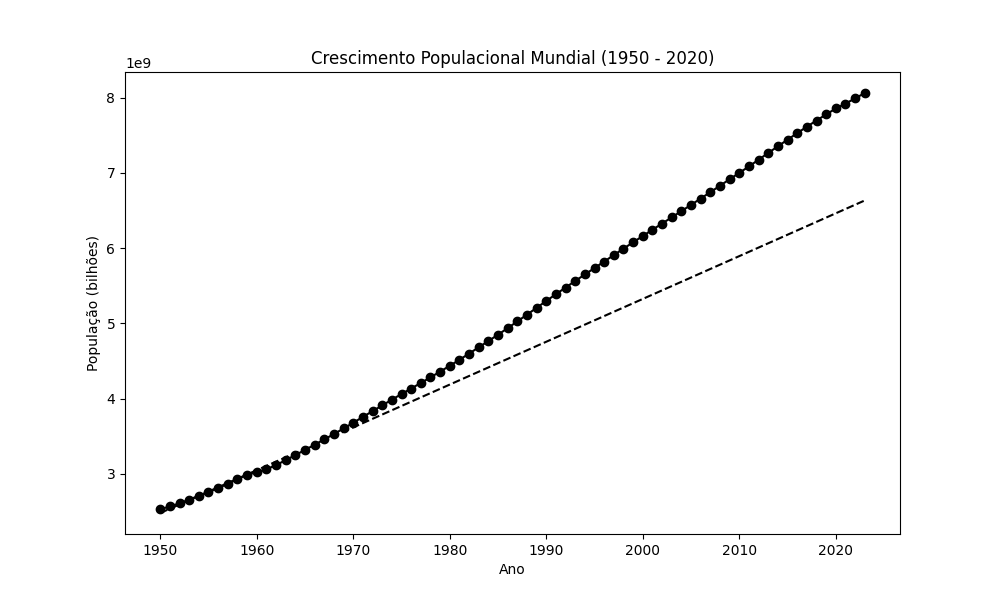
Com o passar dos anos, a linha de ajuste (tracejada) se torna cada vez mais imprecisa, porque os dados não são lineares. A taxa de crescimento não é constante, não segue uma linha reta. Ao extrapolar, podemos ter motivos para acreditar que os dados continuarão a se ajustar à linha. Na prática, normalmente não é assim. Desta forma, concluímos que a interpolação é boa, e a extrapolação é ruim.
Correlação não implica causalidade
Correlação é uma medida estatística que mostra o grau de relação entre duas variáveis. Ela indica se, e como, uma variável muda quando a outra muda. Se ambas variáveis aumentam juntas, observamos uma correlação positiva. Se uma aumenta, enquanto a outra diminui, temos uma correlação negativa. Se não há um padrão, não há correlação.
Temos causalidade quando uma variável afeta diretamente a outra. Ou seja, uma coisa causa a outra.
Um galo canta e o sol nasce. Há correlação? Há causalidade? Os dois eventos são dependentes do tempo: primeiro o galo canta, depois o sol nasce. Então existe uma correlação. Mas isso não implica causalidade: o canto do galo não desencadeia o nascer do sol. Contudo, se essa correlação for observada com frequência suficiente, a mente humana começa a considerar um fato como causador do outro, mesmo quando não há evidências concretas disso.
A ideia de que “correlação não implica causalidade” também se aplica à IA. Existe um caso de IA bastante divulgado, onde o classificador deveria diferenciar huskies e lobos. Embora o modelo demonstrasse bom desempenho com a amostragem de teste, uma investigação demonstrou que o modelo não se concentrava nas imagens dos animais ao tomar as decisões. O modelo percebeu que todas as imagens de treinamento de lobos continham neve em segundo plano, o que não era verdade para as imagens dos huskies. O classificador não aprendeu nada sobre os animais: somente sobre cenários com e sem neve.
Os modelos aprenderam a detectar elementos (presença ou ausência de neve) nos dados de treinamento que se correlacionavam com os alvos pretendidos (cachorros, lobos), mas não aprenderam os alvos em si. Profissionais experientes de machine learning estão atentos a essas correlações ruins. Podemos nos proteger disso utilizando um grande e diversificado conjunto de dados para treinamento e para teste, embora isso nem sempre seja possível. Devemos nos perguntar se nossos modelos aprenderam o que presumimos que aprenderam. E como vimos com os algarismos do MNIST, devemos assegurar que nossos modelos tenham visto todos os tipos de entradas que encontrarão no mundo cotidiano: eles devem interpolar, não extrapolar.
Entendimentos finais (ou iniciais)
Com a conclusão deste post, concluímos também nossa apresentação geral sobre IA (focada em machine learning).
Aprendemos que a IA utiliza-se de modelos, entidades preparadas com muitos dados, para realizar uma tarefa desejada. Entendemos que algumas classificações a serem feitas por IA serão mais fáceis, outras mais difíceis. A qualidade dos resultados do modelo dependerá enormemente de seu treinamento. Se não tomarmos cuidado, o resultado poderá ser enviesado. Se o treinamento não considerar tudo o que a IA encontrará no mundo real, ela não conseguirá responder adequadamente às requisições. E o treinamento deve aprender o que desejamos que ele aprenda, não sendo influenciado por correlações existentes.
Referências
Kneusel, Ronald T.. Como a Inteligência Artificial Funciona: Da Magia à Ciência
Gabriel, Martha. Inteligência Artificial – Do Zero ao Metaverso
Comments (0)