Modelos clássicos de machine learning enfrentam dificuldades com a seleção adequada de features, a dimensionalidade do vetor de feature e a incapacidade de aprender a partir da estrutura inerente à entrada. As redes neurais convolucionais (CNNs) superam essas dificuldades aprendendo a gerar representações novas de suas entradas e, ao mesmo tempo, classificando-as, um processo conhecido como aprendizado end-to-end. CNNs são processadores de dados que usam o aprendizado de representação.
As redes neurais convolucionais exploram a estrutura em suas entradas. Em uma dimensão, as entradas podem ser valores que mudam ao longo do tempo, também conhecidas como séries temporais. Em duas dimensões, estamos falando de imagens. Existem CNNs tridimensionais para interpretar volumes de dados, como uma pilha de imagens de ressonância magnética.
A ordem em que as features são apresentadas a uma rede neural tradicional é irrelevante. Independentemente de apresentarmos vetores de feature ao modelo como (x0, x1, x2) ou (x2, x0, x1), o modelo aprenderá igualmente bem, já que pressupõe que as features são independentes e não relacionadas entre si.
Já as redes neurais convolucionais exploram a estrutura em suas entradas. Para uma CNN, faz diferença se apresentamos a entrada como (x0, x1, x2) ou (x2, x0, x1); o modelo pode aprender bem com a primeira e mal com a segunda. Então faz sentido aplicar as CNNs a situações em que existe estrutura para aprender, que ajuda a determinar a melhor forma de classificar as entradas.
As CNNs decompõem as entradas em pequenas partes, depois em grupos de partes e em grupo ainda maiores de partes, até que toda a entrada seja transformada de um todo em uma representação nova; uma entrada que seja entendida com facilidade pelo equivalente a uma rede neural tradicional. No entanto, mapear a entrada para uma representação nova e entendida com mais facilidade não sugere que os nós compreendam facilmente essa nova representação.
Durante o treinamento, as CNNs aprendem a participar as entradas, possibilitando que camadas superiores da rede sejam classificadas com sucesso; elas aprendem representações novas a partir de suas entradas e, em seguida, classificam essas representações novas.
Convolução é uma operação matemática com definição formal envolvendo cálculo integral. Em nosso caso, trata-se de operações de multiplicação e adição em imagens digitais. A convolução desliza um pequeno quadrado, conhecido como kernel, sobre a imagem, de cima para baixo e da esquerda para a direita. Em cada posição, a convolução multiplica os valores dos pixels sobrepostos pelo quadrado pelos valores correspondentes do kernel. Em seguida, soma todos esses produtos para gerar um único número que se torna o valor do pixel de saída para aquela posição.

A grade de números da esquerda contém os valores de pixel para uma imagem. Os valores estão em gradações de cinza, em um intervalo de 0 a 255, em que valores menores são mais escuros. O kernel é a grade 3 x 3 à direita. A operação de convolução implica em multiplicar cada valor de pixel pelo valor de kernel correspondente. Isso gera a terceira grade de números (mais à direita). A etapa final consiste em somar todos os valores, gerando uma única saída, o número 48, que substitui o pixel central da imagem: 60 -> 48.
A convolução progride deslizando o quadro de 3×3 um pixel para a direita, e repetir o processo. Quando chega ao fim da linha, o quadro é movido um pixel para baixo e repete-se o processo na próxima linha. Processa-se linha alinha até que o kernel tenha sobreposto toda a imagem. A imagem que passou por convolução é a coleção e novos pixels de saída.
A convolução de uma imagem com diferentes kernels destaca aspectos distintos da imagem original.
Redes convolucionais são flexíveis e suportam diversos tipos de camada. Seu fluxo já é conhecido: da entrada para camada após camada, até a saída da rede.
As camadas totalmente conectadas que uma rede neural tradicional usa são chamadas de camadas densas. Em geral, as CNNs usam camadas densas na parte final, perto da saída, pois, nesse momento, a rede já transformou a entrada em uma representação nova, que as camadas totalmente conectadas podem classificar com sucesso. As CNNs fazem uso intenso de camadas convolucionais e de pooling.
As camadas convolucionais aplicam uma coleção de kernels à sua entrada a fim de gerar múltiplas saídas. Os kernels são aprendido durante o treinamento, usando retropropagação e gradiente descendente, vistos em Redes Neurais – Parte 2. Os valores dos kernels aprendidos são os pesos da camada convolucional.
As camadas de pooling não têm pesos associados a elas. Elas executam uma operação fixa em suas entradas: reduzem a extensão espacial de suas entradas, mantendo o maior valor em um quadrado 2 × 2, que é movido sem sobreposição de um lado para o outro e depois para baixo. O resultado final é semelhante à redução do tamanho de uma imagem por um fator de dois.

Uma CNNs típica combina camadas convolucionais e de pooling antes de concluir o fluxo com uma ou duas camadas densas. As camadas ReLU também são usadas, normalmente após as camadas convolucionais e densas. Por exemplo, a rede LeNet é composta das seguintes camadas:

O número entre parênteses para cada camada convolucional é o número de filtros a serem aprendidos nessa camada. Um filtro é uma coleção de kernels convolucionais, com um kernel para cada canal de entrada. Por exemplo, a primeira camada convolucional aprende 6 filtros. A entrada é uma imagem em escala de cinza com um canal. Desse modo, essa camada aprende 6 kernels. A segunda camada convolucional aprende 16 filtros, cada um com 6 kernels, 1 para cada um dos 6 canais de entrada da primeira camada convolucional. Portanto, a segunda camada convolucional aprende um total de 96 kernels. Por último, a última camada convolucional aprende 120 filtros, cada um com 16 kernels, para outros 1.920 kernels. No total, o modelo LeNet precisa aprender 2.022 kernels convolucionais diferentes.
Espera-se que o aprendizado de tantos kernels gere uma sequência de saídas que capture elementos essenciais das estruturas de entrada. Se o treinamento for bem-sucedido, a saída da camada convolucional final conterá valores que diferenciam claramente as classes.
A figura abaixo mostra como um modelo LeNet, treinado nos algarismos do MNIST, manipula duas imagens de entrada. A saída da primeira camada convolucional são as 6 imagens intermediárias, em que o cinza representa zero, os pixels mais escuros são cada vez mais negativos e os pixels mais claros são cada vez mais positivos. Cada um dos seis kernels da primeira camada convolucional gera uma imagem de saída para a única imagem de entrada. Os kernels destacam diferentes partes das entradas como transições do escuro para o claro.
O padrão semelhante a um código de barras mais à direita é uma representação da saída da camada densa. Estamos ignorando a saída da segunda e da terceira camadas convolucionais, indo diretamente para o final do modelo. A saída da camada densa é um vetor de 84 números. Para esta figura, esses números foram mapeados para valores de pixel, em que os valores maiores correspondem às barras verticais mais escuras.
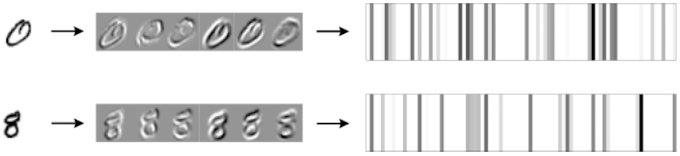
Os códigos de barra para 0 e 8 são diferentes. Mas, os códigos de barra compartilham semelhanças para os mesmos algarismos? Sim, veja abaixo.
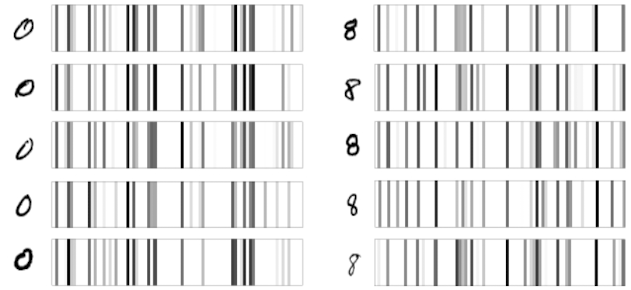
Os códigos de barra não são idênticos, mas compartilham similaridades de acordo com o algarismo. O modelo LeNet aprendeu a mapear a imagem de entrada 28 x 28 pixels (784 pixels) em um vetor de 84 números, que apresenta similaridade por tipo de algarismo. Percebemos que esse mapeamento gerou algo de menor dimensionalidade, que preserva as diferenças entre os algarismos. O modelo treinado aprendeu a “ver” o mundo dos algarismos manuscritos, representados como pequenas imagens em escalas de cinza.
As camadas CNN anteriores à camada densa aprenderam a se comportar como uma função, gerando um vetor de saída a partir da imagem de entrada. O verdadeiro classificador é a camada densa, que funciona bem, já que a CNN aprendeu o classificador (camada densa) enquanto aprendia simultaneamente a função de mapeamento.
Ao aprenderem a representar partes de um objeto em uma imagem, é possível aprender uma representação nova (chamada embedding) que as camadas densas da rede podem classificar com sucesso.
Como escolher a arquitetura de uma CNN
Digamos que você tem um conjunto de dados e precisa criar uma CNN. Qual arquitetura deve usar? De quais camadas você precisa e em que ordem? É necessário usar kernels convolucionais 5 × 5 ou 3 × 3? Quantas épocas de treinamento são suficientes? De início, antes do desenvolvimento de arquiteturas padrão, cada uma dessas perguntas precisava ser respondida pela pessoa que arquitetava a rede. Alguns começaram a questionar se o software seria capaz de determinar de forma automática a arquitetura do modelo e os parâmetros de treinamento. Assim nasceu o machine learning automático, ou AutoML.
Referências
Kneusel, Ronald T.. Como a Inteligência Artificial Funciona: Da Magia à Ciência
Comments (0)